La primera parte importante al entrar en el terreno de los rines, llantas y neumáticos de una bicicleta es una parte del neumático que en inglés se llama "bead". El traductor de Google define esta palabra como "the reinforced inner edge of a pneumatic tire that grips the rim of the wheel". Lo cuál traduce más o menos lo siguiente: es el borde interior reforzado de un neumático que se adhiere al rin (de la rueda). La traducción directa es "talón", así que lo llamaré el talón, así seguramente tenga una traducción mejor. También encuentro al leer que al parecer la palabra "bead" no se refiere al neumático (a la cámara como también lo llaman en algunos paises de habla hispana), sino que se refiere a la parte reforzada de la llanta que ajusta contra las caras interiores del rin. Por videos que he visto a menudo cuando una llanta pierde el aire o cuando se desea cambiar llanta o neumático o reparar una llanta baja debida a un "pinchazo" (aunque en Colombia se suele decir que la llanta "se chuzó"), este borde "se destalona", por lo que pienso que la segunda definición de talón convence más, así que cuando lean "talón" mejor piensen en los bordes de las llantas que está en contacto con el rin. Este talón forma un círculo, y es el diámetro de este círculo el que determina el ajuste de la llanta y el rin.
Hablando un poco de la nomenclatura, diferentes paises pueden usar una diferente.
Marcado británico
Los números son una nomenclatura de referencia y no deben tomarse como medidas exactas. El primer número es el diámetro nominal de la llanta y el segundo es la altura nominal de la llanta. El primer número coincide aproximadamente con el diámetro exterior de la llanta cuando está llena de aire. Ejemplo:
| 26'' x 1.5'' | Diámetro nominal de la llanta 26 pulgadas x Altura nominal de la llanta 1.5 pulgadas |
| 27.5'' x 2.25'' | Diámetro nominal de la llanta 27.5 pulgadas x Altura nominal de la llanta 2.25 pulgadas |
Marcado Francés
Los números también son sólo una referencia y no corresponden a una medida en particular. Llantas de ruta 700c tienen un diámetro de talón de 622 mm. El primer número indica referencia para el diámetro exterior de la llanta cuando está inflada y el segundo número es la referencia para el ancho nominal entre paredes del rin. Ejemplo:
| 700 x 25C | Diámetro nominal de la llanta 700 mm x Ancho nominal 25C |
Marcado según ISO 5775 o ETRTO
El sistema ETRTO (European Tire and Rim Technical Organization) es el mismo sistema ISO 5775, y usa dos números. El número más grande es siempre el diámetro de contacto del talón de la llanta con el rin. El número ETRTO más pequeño es el ancho en milímetros entre las paredes interiores (paralelas) del rin. Ejemplos:
| ETRTO 25-622 | Diámetro de talón 622 mm y ancho nominal 25 mm |
| ETRTO 584x21 | Diámetro de talón 584 mm y ancho nominal 21 mm |
Una regla para el ancho de la llanta en ISO es un ancho entre 1.5 y 2 veces el ancho ISO del rin. Un ancho de rin ISO de 25 mm debería usarse con un ancho de llanta ISO aproximado entre 37 y 50 mm. Las llantas y rines fabricados para acoplarse tienen la misma designación (el mismo número). Por ejemplo: llantas marcadas 622 ajustarán sobre rines marcados 622, dado que el diámetro de contacto del talón de la llanta con el rin es de 622 mm en ambos. A continuación, un par de tamaños comunes:
Tabla 1. Tamaños de llantas (sólo dos ejemplos).
|
Nomenclatura común |
Diámetro del talón ETRTO o ISO |
Uso común |
|
29'' |
622 | Bicicletas de montaña (MTB) |
|
16'' x 1'' hasta 16'' x 2.2'' |
305 | Bicicletas para niños |
Longitud de los radios de una rueda para bicicleta
A continuación se presenta una formula para el cálculo de la longitud de los radios que unen el eje (hub) con el rin de la llanta de una bicicleta. Se reduce a un problema de trigonometría. Primero, se calcula la longitud del lado \(C\) del triángulo usando la ley de cosenos:
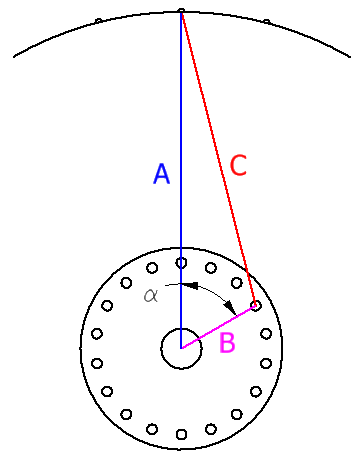
Figura 1. Triángulo para el cálculo de la longitud de un radio usando la ley de cosenos.
$$ C = \sqrt{A^2+B^2-2AB \cos \alpha} $$
Ec. 1
Donde:
- \(A\) y \(B\) son los lados conocidos que pueden medirse usando instrumentos.
- \(\alpha\) es el ángulo entre los lados \(A\) y \(B\).
El ángulo \(\alpha\) depende del número de agujeros para los radios y de la disposición de los radios al ensamblar. Se debe tener en cuenta que el triángulo ABC anterior está en el mismo plano que los orificios para los radios que tiene el rin, lo cual aún no brinda la medida requerida de la longitud del radio, dado que estos no van radiales sino con un ángulo con respecto a dicho plano, el cual generalmente es diferente a un lado y al otro. Por esta razón, se requiere de un segundo paso, donde calculamos la longitud \(L\) del radio en función de \(C\) y la distancia \(w\) indicadas por la línea azul o por la línea verde en la Figura 2. Se introduce una corrección al restar al cálculo mediante el teorema de Pitágoras la mitad del diámetro de los agujeros para los radios del eje (ver Ec. 2).
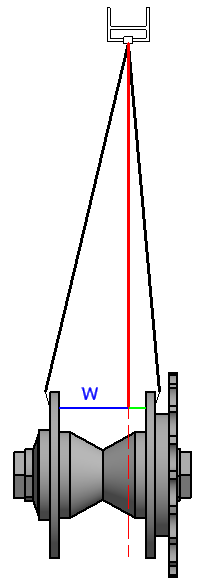
Figura 2. Construcción para el segundo paso de cálculo de la longitud de un radio usando el teorema de Pitágoras.
$$ L = \sqrt{C^2+w^2} - \frac{d}{2} $$
Ec. 2
Donde:
- \(C\) es el resultado de la Ec. 1 (ver Fig. 1).
- \(w\) es la distancia dada por las líneas azul o verde en la Fig. 2.
- \(d\) es el diámetro de los agujeros para los radios maquinados en el eje.




Comentarios potenciados por CComment