These are works that I have done in the past. Most of them are documents that I have elaborated during my studies..

Constitutive relations for plane stress material with transverse shear deformations

Notes: here are some notes of constitutive relations, starting with linear elastic anisotropic material model. Notes focus on finding the constitutive relation for a plane stess material model that includes transverse shear deformation. This kind of material model is used in plates and shells that use an orthotropic material where stress sigma33 is assumed to be zero and includes shear modulus G23 and G13. Latex files of the .pdf document can be downloaded here.

Parallel computing

TP1: Message Passing Interface - MPI: Sum of vectors.

TP2: Message Passing Interface - MPI: matrix vector multiplication, Conjugated Gradient algorithm and Jacobi pre-conditioning to solve a system of equations, code speed-up analysis.

TP3: Parallel programming using OpenMP.

TP4: Parallel programming using CUDA (Nvidia).

TP5: Tumor ablation using Irreversible Electroporation -IRE- using computational models (COMSOL).

Basics of finite element analysis

FEM TP1: Weak formulations.

FEM TP2: Shape functions.

FEM TP3: Heat transfer.

FEM TP4: Linear elasticity.

FEM TP5: Unidimensional transient heat transfer analysis.

FEM TP6: Convection - Diffusion problem.

FEM TP7: Two dimensional heat transfer analysis - Heat exchanger.

Finite element analysis - Solids

TP1: Non-linear system solution: convergence criteria, Newton-Rhapson, BFGS.

TP2: Total Lagrangian Formulation problem.

TP3: Von-mises elasto-plasticity problem.

Neural networks

TP1: Hopfield 82 neural network.

TP2: Simple and multilayer perceptron, and multilayer perceptron with backpropagation.

TP3: Kohonen neural network.

TP4: Perceptron with backpropagation applied to constitutive relation prediction

Basic notes on continuum mechanics

Continua: deformation gradient tensor, second piola-kirchhoff stress tensor, green-lagrange strain tensor.

Elasto-plasticity: Von Mises plasticity, hardening law, strain hardening modulus, perfect plasticity, kinematic hardening, radial return algorithm.

Plane strain and plain stress: the two material models.

Tensors: some theory about tensor algebra.

Numeric analysis

TP1: Numerical solution of unidimensional wave equation.

TP2: Finite volume solution to heat transfer problem - Heat exchanger.

Digital Control

TP1: basic concepts of digital control.

Papers in conference proceedings

Simposio nacional en mecánica de materiales y estructuras contínuas: experimentación, modelado numérico y teórico - SMEC 2014 (download conference proceedings from conference website): Redes neuronales aplicadas al entrenamiento de relaciones constitutivas lineales y no lineales.

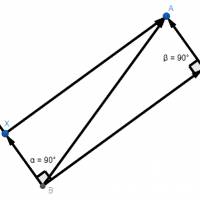
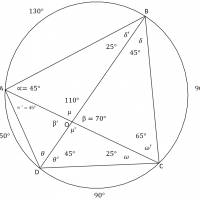
Euclidean Geometry

Some exercises about congruence and similarity of triangles and the demonstration of Pitagora's theorem can be downloaded here. Latex files can downloaded here.

Some excercises about circumference can be found here and the latex files here.