3. (Dificultad: 6/10) Determinar si el siguiente límite existe. En caso de existir, calcularlo:
$$ \lim_{x \to 1} \frac{ \left| x^2-1 \right| }{x-1} $$
SOLUCIÓN
Se debe recordar que:
$$ \left| x^2-1 \right| = x^2-1~~~\text{si}~~~x^2-1 \ge 0 $$
$$ \left| x^2-1 \right| = -\left( x^2-1 \right)~~~\text{si}~~~x^2-1 < 0 $$
Interesa entonces saber para qué intervalos la función que se encuentra entre las barras de valor absoluto es menor que cero, mayor que cero o igual a cero. Para ello se puede factorizar y evaluar cada factor en los intervalos que resultan de hallar los ceros de la función, así:
$$ x^2-1 = 0 $$
Se desarrolla la diferencia de cuadrados, quedando:
$$ (x+1)(x-1) = 0 $$
La solución de esta ecuación es:
$$ x+1=0~\rightarrow~x=-1~~~\text{Ec.1}$$
$$ x-1=0~\rightarrow~x=1~~~\text{Ec.2}$$
Se evalúa cada factor para determinar el signo que tiene en cada intervalo:
| $$ -\infty $$ | ------ | -1 | ------ | +1 | ------ | $$+\infty $$ | |
| $$ (x+1) $$ | - | + | + | ||||
| $$ (x-1) $$ | - | - | + | ||||
| $$ (x+1)(x-1) $$ | + | - | + |
Recordemos de nuevo las condiciones para poder sustituir la función con las barras de valor absoluto por una expresión sin las barras de valor absoluto:
Condición 1
$$ \left| x^2-1 \right| = x^2-1~~~\text{si}~~~x^2-1 \ge 0 $$
Lo anterior se cumple para todo valor de \(x\) perteneciente al conjunto:
$$ (-\infty,-1]~U~[1,\infty) $$
Nótese que los intervalor están cerrados en -1 y 1, ya que en la Ec.1 y Ec.2 se pudo demostrar que \(x=-1\) y \(x=1\) también satisfacen esta condición. Por lo anterior, cuando \(x\) tiende a 1 por la derecha la función \(x^2-1>0\) y en consecuencia \( \left| x^2-1 \right| = \left(x^2-1\right) \).
Condición 2
$$ \left| x^2-1 \right| = -\left( x^2-1 \right)~~~\text{si}~~~x^2-1 < 0 $$
Lo anterior se cumple para todo valor de \(x\) perteneciente al conjunto:
$$ (-1,1) $$
Por lo anterior, cuando \(x\) tiende a 1 por la izquierda la función \(x^2-1<0\) y en consecuencia \( \left| x^2-1 \right| = -\left(x^2-1\right) \).
Límite por la izquierda
Teniendo en cuenta lo anterior, se escribe:
$$ \lim_{x \to 1^-} \frac{-(x^2-1)}{x-1} $$
$$ \lim_{x \to 1^-} \frac{-(x+1)(x-1)}{x-1} $$
$$ \lim_{x \to 1^-} -(x+1) $$
$$ \lim_{x \to 1^-} -x-1 = -1-1 = -2$$
Límite por la derecha
Teniendo en cuenta lo anterior, se escribe:
$$ \lim_{x \to 1^+} \frac{(x^2-1)}{x-1} $$
$$ \lim_{x \to 1^+} \frac{(x+1)(x-1)}{x-1} $$
$$ \lim_{x \to 1^+} (x+1) $$
$$ \lim_{x \to 1^+} x+1 = 1+1 = 2$$
Debido a que los límites cuando x tiende a 1 por la izquierda y por la derecha son diferentes, el límite no existe.
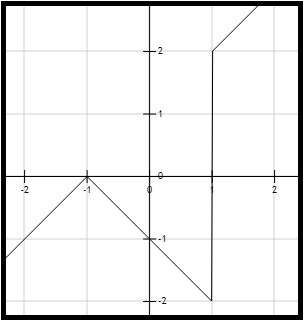
Figura 1. Gráfica de la curva de la función \( \frac{ \left| x^2-1 \right| }{x-1} \).




Comentarios potenciados por CComment