Ejercicio 19 | Distancia entre dos rectas en R3

Hallar la distancia entre las dos rectas:

$$ \overleftrightarrow{L_1}:~\frac{x-2}{3}=y+1=\frac{z}{2} $$

$$ \overleftrightarrow{L_2}:~x = \frac{y-1}{2} = \frac{z+3}{4} $$

Solución

Las ecuaciones simétricas de las rectas \(\overleftrightarrow{L_1}\) y \(\overleftrightarrow{L_2}\) se pueden reescribir como:

$$ \overleftrightarrow{L_1}:~\frac{x-2}{3}=\frac{y-(-1)}{1}=\frac{z-0}{2} $$

$$ \overleftrightarrow{L_2}:~\frac{x-0}{1} = \frac{y-1}{2} = \frac{z-(-3)}{4} $$

De ellas se pueden obtener los puntos que pertenecen a las rectas y los vectores directores.

Para \(\overleftrightarrow{L_1}\):

$$ P_1(2,-1,0) $$

$$ \overrightarrow{d_1}=(3,1,2) $$

Para \(\overleftrightarrow{L_2}\):

$$ P_2(0,1,-3) $$

$$ \overrightarrow{d_2}=(1,2,4) $$

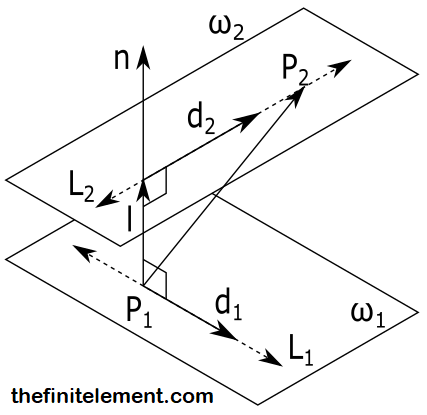
Para hallar la distancia entre dos rectas es necesario recordar la definición de la distancia entre un punto y una recta, la cual es la medida del segmento que va desde el punto hasta la recta, llegando perpendicular sobre la recta. En este caso, es necesario pensar que esta situación se repite dos veces, una para cada recta, con un punto sobre cada recta. De este modo, es necesario visualizar la distancia entre dos rectas como la medida del segmento que va desde un punto de una recta hasta un punto de la otra recta, pero en ambas, ese punto es el pie de una perpendicular. Se requiere, entonces, garantizar, mediante una operación vectorial, dicha perpendicularidad a ambas rectas. Aquí entra en juego el producto vectorial o producto cruz entre los dos vectores directores:

$$ \overrightarrow{n} = \overrightarrow{d_1} \times \overrightarrow{d_2} $$

$$ \overrightarrow{n} = (3,1,2) \times (1,2,4) $$

$$ \overrightarrow{n} = \left[ (1)(4) - (2)(2) \right] \hat{i} + \left[ (2)(1) - (3)(4) \right] \hat{j} + \left[ (3)(2) - (1)(1) \right] \hat{k} $$

$$ \overrightarrow{n} = 0 \hat{i} - 10 \hat{j} + 5 \hat{k} $$

$$ \overrightarrow{n} = (0,-10,5) $$

La operación anterior resultó en un vector \(\overrightarrow{n}\) perpendicular a ambos vectores \(\overrightarrow{d_1}\) y \(\overrightarrow{d_2}\) y, por ende, perpendicular a ambas rectas. Podemos ahora imaginar dos planos que contienen a cada una de las rectas. Estos planos pueden definirse usando el vector normal (\overrightarrow{n}\) hallado, luego, los planos serían paralelos.

Ahora, se debe pensar en que se tienen los puntos \(P_1(2,-1,0)\) y \(P_2(0,1,-3)\) para cada recta. Será posible, entonces, hallar un vector definido por estos dos puntos y proyectarlo sobre el vector \(\overrightarrow{n}\) para así obtener la distancia entre las dos rectas requerida:

$$ \overrightarrow{P_1P_2} = \overrightarrow{P_2}-\overrightarrow{P_1} = (2,-1,0)-(0,1,-3) $$

$$ \overrightarrow{P_1P_2} = (2,-2,3) $$

La proyección ortogonal del vector \(\overrightarrow{P_1P_2}\) sobre el vector \(\overrightarrow{n}\) es:

$$ \overrightarrow{l} = Proy_{\overrightarrow{n}} \overrightarrow{P_1P_2} = \left( \frac{\overrightarrow{n} \cdot \overrightarrow{P_1P_2}}{\overrightarrow{n} \cdot \overrightarrow{n}} \right) \overrightarrow{n} $$

$$ \overrightarrow{l} = Proy_{\overrightarrow{n}} \overrightarrow{P_1P_2} = \left( \frac{(0,-10,5) \cdot (2,-2,3)}{(0,-10,5) \cdot (0,-10,5)} \right) (0,-10,5) $$

$$ \overrightarrow{l} = \frac{7}{25} (0,-10,5) $$

$$ \overrightarrow{l} = (0,-14/5,7/5) $$

La distancia entre las dos rectas es la magnitud del vector \(\overrightarrow{l}\):

$$ \| \overrightarrow{l} \| = \sqrt{(-14/5)^2+(7/5)^2} $$

$$ \| \overrightarrow{l} \| = \sqrt{\left(\frac{49}{5}\right)} = 3.13 $$