26. Hallar la ecuación general del plano que pasa por el punto P de intersección de la recta
$$ \overleftrightarrow{l}: \frac{x-1}{2}=\frac{y}{2}=\frac{z-1}{-1} $$
con el plano
$$ \pi_1: x-2y+5z+1=0 $$
y contiene a la recta \( \overleftrightarrow{r} \) de intersección de los planos
$$ \pi_2: x+y-z=2 $$
y
$$ \pi_3: 2x-y+3z=1 $$
DESARROLLO
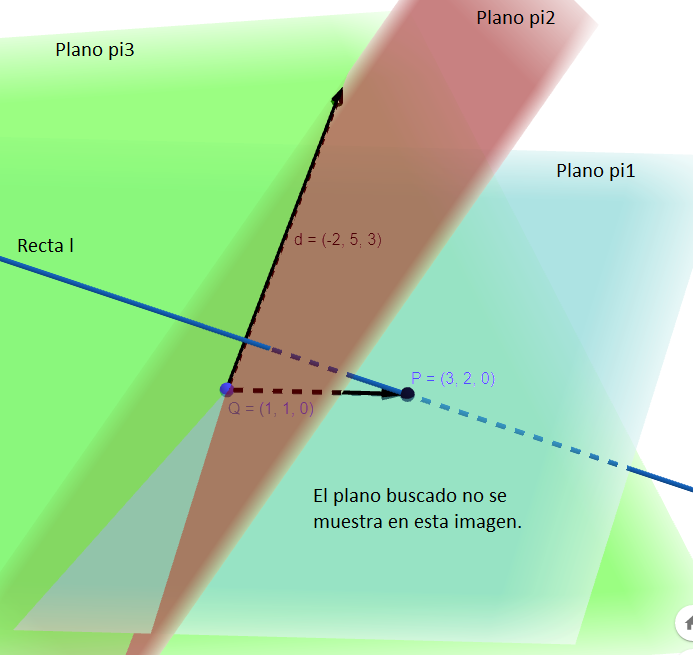
Primero, hallemos el punto que tienen en común la recta \( \overleftrightarrow{l} \) y el plano \( \pi_1 \). El procedimiento detallado se puede encontrar en el ejercicio 16 de este mismo taller:
Geometría analítica | Solución ejercicio 16 | Rectas y planos
Lo describiré de igual forma así: escribimos las ecuaciones paramétricas de la recta \( \overleftrightarrow{l} \), las cuales quedarán con x, y, z como variables dependientes y en función de un parámetro. Luego, sustituímos estas ecuaciones para x, y, z en la ecuación general del plano \( \pi_1 \). Obtendremos una ecuación con una incógnita, que será el parámetro. Resolvemos para el parámetro, que resulta t=1 y luego lo sustituimos en las ecuaciones paramétricas de la recta \( \overleftrightarrow{l} \) para obtener el punto:
$$ P(x,y,z)=P(3,2,0) $$
A continuación hallaremos un vector director para la recta de intersección entre los planos \( \pi_2 \) y \( \pi_3 \), el cual se puede obtener del producto cruz entre los dos vectores normales a estos planos, que se obtienen de los coeficientes que acompañan a las variables x, y, z en las ecuaciones generales de cada plano. El orden en que se realice el producto de los dos vectores normales es indiferente, dado que ambos serán paralelos a la recta de intersección.
$$ \overrightarrow{d} = \overrightarrow{n}_2 \times \overrightarrow{n}_3 = (1, 1, -1) \times (2, -1, 3) $$
El vector director de la recta de intersección entre ambos planos es:
$$ \overrightarrow{d} = (-2, 5, 3) $$
Para resolver el problema, se quiere realizar un producto cruz entre dos vectores paralelos al plano, de modo que el vector resultante sea perpendicular a ellos y lo podamos tomar como el vector normal del plano que estamos buscando. Ya tenemos un vector paralelo al plano, el cual es el vector director que acabamos de encontrar. Necesitamos otro. Para definirlo, tenemos ya un punto que también pertenece al plano -aquél que nos da el problema- pero necesitamos otro punto, al cual llamaremos Q. Encontremos entonces un punto que pertenezca a la recta \( \overleftrightarrow{r} \). Para ello, impondremos un valor cualquiera a una de las coordenadas, por ejemplo, z=0. Con esto estamos reduciendo el conjunto solución de ambos planos a dos rectas, en cuya intersección estará el punto de interés. Trabajando con las ecuaciones de los planos pi2 y pi3 resultará:
$$ Para~\pi_2:~~~x+y=2 $$
$$ Para~\pi_3:~~~2x-y=1 $$
Se obtiene un sistema de ecuaciones de 2 x 2. Al resolverlo, resulta:
$$ x=1 $$
$$ y=1 $$
Es decir, un punto -de infinitos- que pertenece a la recta de intersección de ambos planos es:
$$ Q(x,y,z)=Q(1,1,0) $$
El otro vector paralelo al plano buscado resultará de usar los puntos Q y P para formar un vector QP, dado que ambos puntos pertenecen al plano buscado.
$$ \overrightarrow{QP} = \overrightarrow{P} - \overrightarrow{Q} = (3,2,0)-(1,1,0) $$
$$ \overrightarrow{QP} = (2,1,0) $$
Con los dos vectores paralelos al plano, d y QP, hallamos el vector normal al plano buscado:
$$ \overrightarrow{n} = \overrightarrow{d} \times \overrightarrow{QP} = (-2,5,3) \times (2,1,0) $$
$$ \overrightarrow{n} = (-3,6,-12) $$
La ecuación general del plano se puede hallar a partir de la forma normal:
$$ \overrightarrow{n} \cdot \overrightarrow{x} = \overrightarrow{n} \cdot \overrightarrow{p} $$
Esto resulta:
$$ (-3,6,-12) \cdot (x,y,z) = (-3,6,-12) \cdot (3,2,0) $$
$$ -3x+6y-12z=-9+12=3 $$
La ecuación anterior se puede escribir mejor si aplicamos propiedades de los reales (de las igualdades), multiplicando a ambos lados por -1/3, resultando:
$$ x-2y+4z=-1 $$
Cualquier otra forma que resulte de multiplicar esta expresión a ambos lados por un número real también es aceptable.




Comentarios potenciados por CComment