7g. Hallar la ecuación del plano que pasa por el punto \(P(-1,2,1) \) y contiene la recta de intersección de los planos \(\pi_1: x+y-z=2\) y \(\pi_2: 2x-y+3z=1\).

Desarrollo

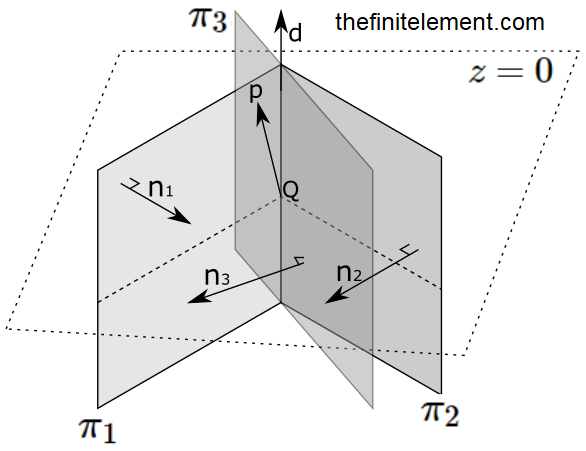
El problema se puede resolver hallando primero un vector director que resulta de calcular el producto vectorial (producto cruz) entre los vectores normales a los planos, que pueden obtenerse de las dos ecuaciones para los planos \(\pi_1\) y \(\pi_2\). Posteriormente, se halla un punto que esté contenido en la recta de intersección de ambos planos, para luego definir un vector paralelo al plano que sea útil para hallar un vector normal al plano solicitado por el problema.

Las componentes de los vectores normales a los planos se pueden obtener de los coeficientes que acompañan a las variables \(x, y, z\) en las dos ecuaciones generales de los planos \(\pi_1\) y \(\pi_2\), así:

$$ \text{Para}~\pi_1: \overrightarrow{n_1}=(1,1,-1) $$

$$ \text{Para}~\pi_2: \overrightarrow{n_2}=(2,-1,3) $$

Ahora, hallamos un vector director para la recta de intersección de los planos \(\pi_1\) y \(\pi_2\). Este vector director será paralelo a la recta. Calculamos para ello el siguiente producto vectorial:

$$ \overrightarrow{d} = \overrightarrow{n_2} \times \overrightarrow{n_1} $$

$$ \overrightarrow{d}=  (2,-1,3) \times (1,1,-1) = [(-1)(-1)-(3)(1)] \overrightarrow{i} $$

$$ + [(3)(1)-(2)(-1)] \overrightarrow{j} + [(2)(1)-(-1)(1)] \overrightarrow{k} $$

$$ \overrightarrow{d}=  -2 \overrightarrow{i} + 5 \overrightarrow{j} + 3 \overrightarrow{k} $$

$$ \overrightarrow{d}=  (-2,5,3) $$

Luego, se puede hallar un punto sobre la recta de intersección de \(\pi_1\) y \(\pi_2\), tomando las ecuaciones generales de cada plano y haciendo \(z=0\) en ambas. Esto definirá un plano \(z=0\) que cortará a ambos planos.

$$ \text{Para}~\pi_1~y~z=0:~x+y=2~~~(Ec. 1) $$

$$ \text{Para}~\pi_2~y~z=0:~2x-y=1~~~(Ec. 2) $$

Resolvemos el sistema de ecuaciones anterior sumándolas, lo cual resulta:

$$ 3x=3 $$

$$ x=1~~~(Ec. 3)$$

Se sustituye la Ec. 3 en la Ec. 1 para obtener:

$$ y=1~~~(Ec. 4) $$

Al hacer \(z=0\) y resolver el sistema de ecuaciones de 2 x 2 se acaba de obtener un punto \(Q(1,1,0)\), el cual es el punto en donde el plano \(z=0\) corta a la recta de intersección entre los planos \(\pi_1\) y \(\pi_2\). Las ecuaciones Ec. 1 y Ec. 2 son las rectas en \(R^2\) que corresponden a las intersecciones de los planos \(\pi_1\) con el plano \(z=0\) y los planos \(\pi_2\) con el plano \(z=0\). Posteriormente, se define un vector:

$$ \overrightarrow{QP} = \overrightarrow{P} - \overrightarrow{Q} = (-1,2,1)-(1,1,0)$$

$$ \overrightarrow{QP} = (-2,1,1) $$

Dado que el plano pasa por el punto \(P\) y el punto \(Q\) está contenido en la recta de intersección de \(\pi_1\) y \(\pi_2\), el vector \(\overrightarrow{QP}\) es paralelo al plano que se quiere hallar, el cual se denominará \(\pi_3\). Para hallar dicho plano se puede usar la forma normal de la ecuación de un plano en \(R^3\), para lo cual se requiere de un vector normal \(\overrightarrow{n_3}\) y de un punto contenido en el plano, el cual ya se tiene y es \(P\). El vector normal se puede hallar así:

$$ \overrightarrow{n_3} = \overrightarrow{QP} \times \overrightarrow{d} $$

El resultado de esta operación es:

$$ \overrightarrow{n_3} = (-2,4,8) $$

Ahora, se usa la forma normal de la ecuación de un plano en \(R^3\):

$$ \overrightarrow{n_3} \cdot \overrightarrow{x} = \overrightarrow{n_3} \cdot \overrightarrow{p} $$

Donde \(\overrightarrow{p}\) es un vector cuyas componentes son las coordenadas del punto \(P\), es decir, un vector con la cola en el origen y cabeza en el punto \(P\). Luego:

$$ (-2,4,-8) \cdot (x,y,z) = (-2,4,-8) \cdot (-1,2,1) $$

Operando, queda:

$$ -2x+4y-8z=2$$

Dividiendo a ambos lados sobre 2:

$$ -x+2y-4z=1 $$

La anterior es la ecuación del plano buscada. Si se multiplica a ambos lados por -1 se puede obtener otra ecuación para el mismo plano:

$$ x-2y+4z=-1 $$

Esta última es la ecuación que se halla como respuesta de este problema.