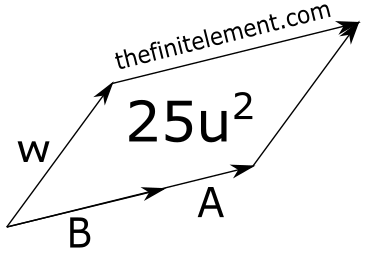
18. Hallar un vector \(\overrightarrow{A}\) en la misma dirección del vector \(\overrightarrow{B}=\hat{i}-2\hat{j}+3\hat{k}\) que determine con el vector \(\overrightarrow{w}=-2\hat{i}+4\hat{j}-\hat{k}\) un paralelogramo de área 25 unidades cuadradas.
Solución
Se posee:
$$ \overrightarrow{B}=(1,-2,3) ~~~\text{Ec. 1}$$
$$ \overrightarrow{w}=(-2,4,-1) ~~~ \text{Ec. 2} $$
$$ \text{Área}=25 ~~~\text{Ec. 3}$$
Si el vector \(\overrightarrow{A}\) tiene la misma dirección que el vector \(\overrightarrow{B}\), entonces el vector \(\overrightarrow{A}\) puede escribirse como:
$$ \overrightarrow{A}= t \overrightarrow{B}~~~\text{Ec. 4}$$
Siendo \(t\) un escalar. También es necesario recordar que se puede demostrar que el área de un paralelogramo en R3 puede definirse por dos vectores. En este caso, los vectores que definen el paralelogramo en R3 son \(\overrightarrow{A}\) y \(\overrightarrow{w}\), y su área se puede calcular resolviendo:
$$ \text{Área} = \| \overrightarrow{w} \times \overrightarrow{A} \| = \| \overrightarrow{w} \| \| \overrightarrow{A} \| \sin \theta~~~\text{Ec. 5} $$
Escribimos entonces, de 2 y 4 en 5:
$$ 25 = \| \overrightarrow{w} \times \overrightarrow{A} \| = \| \overrightarrow{w} \times t \overrightarrow{B} \| $$
Se puede calcular primero el producto cruz y aprovechar una propiedad del álgebra vectorial asociada al producto cruz (puede demostrarse fácilmente) que consiste en sacar al escalar \(t\) fuera del paréntesis:
$$ \overrightarrow{w} \times \overrightarrow{A} = \overrightarrow{w} \times t \overrightarrow{B} = t ( \overrightarrow{w} \times \overrightarrow{B} ) $$
$$ \overrightarrow{w} \times \overrightarrow{A} = t ( (-2,4,-1) \times (1,-2,3) ) $$
$$ \overrightarrow{w} \times \overrightarrow{A} = t ( \left[ (4)(3)-(-1)(-2) \right] \hat{i} + \left[ (-1)(1)-(-2)(3) \right] \hat{j} + \left[ (-2)(-2)-(4)(1) \right] \hat{k} ) $$
$$ \overrightarrow{w} \times \overrightarrow{A} = t ( \left[ 12-2 \right] \hat{i} + \left[ -1+6 \right] \hat{j} + \left[ 4-4 \right] \hat{k} ) $$
$$ \overrightarrow{w} \times \overrightarrow{A} = t ( \left[ 10 \right] \hat{i} + \left[ 5 \right] \hat{j} + \left[ 0 \right] \hat{k} ) $$
Ahora, se calcula la magnitud del producto cruz usando una propiedad para hallar la magnitud de un vector por un escalar, que consiste en calcular el valor absoluto del escalar y multiplicarlo por la magnitud del vector:
$$ \| \overrightarrow{w} \times \overrightarrow{A} \| = |t|~ ( \sqrt{ 10^2 + 5^2 + 0^2 } ) = |t| \sqrt{125} = 5 |t| \sqrt{5} $$
Dado que la magnitud del producto cruz es igual al área del paralelogramo, podemos igualar a 25:
$$ 5 |t| \sqrt{5} = 25 $$
Dado que 25 y \(\sqrt{5}\) son positivos, podemos escribir:
$$ t = \frac{25}{5 \sqrt{5}} = \frac{5 \sqrt{5}}{5}$$
Finalmente:
$$ t = \sqrt{5} $$
De 4, se obtiene la respuesta a este problema:
$$ \overrightarrow{A} = t (1,-2,3) $$
$$ \overrightarrow{A} = (\sqrt{5},-2 \sqrt{5},3 \sqrt{5}) $$




Comentarios potenciados por CComment