Visto: 3575

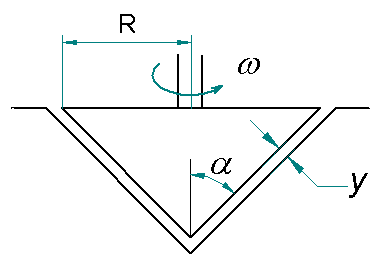
Calcular el momento torsional necesario para hacer girar el cono mostrado en la Figura 1 a una velocidad ω constante si un fluido de viscosidad μ llena el espacio entre él y la superficie cónica. Dicha separación tiene un valor de "y", el radio del cono es R y el ángulo que forma la pared con la vertical es α.

 

Figura 1.

Desarrollo

1. La expresión para el esfuerzo cortante es:

\[ \tau = \mu \frac{du}{dy} \]

Luego, tenemos que el esfuerzo es igual a un diferencial de fuerza sobre un diferencial de área,

\[ \frac{dF}{dA} = \mu \frac{du}{dy} \]

Debido a que la separación entre las superficies es muy pequeña podemos decir que,

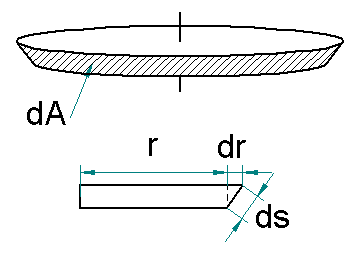
\[ \frac{du}{dy}=\frac{\Delta u}{\Delta y} = \frac{\omega . r - 0}{y-0} = \frac{\omega . r}{y} \]

Ahora, tomando el diferencial de área aproximadamente como una cinta cónica, como se aprecia en la Figura 2, decimos que,

\[ dA = 2 \pi r ~ds = 2 \pi r \frac{dr}{\sin \alpha} \]

Figura 2. Tomando el diferencial de área.

Sabiendo de antemano que,

\[ \sin \alpha = \frac{dr}{ds} \]

Luego, tenemos la expresión para dF al reemplazar du/dy y dA.

\[ dF = \frac{2 \pi \mu \omega}{y \sin \alpha} r^2~dr \]

Tomando la ecuación diferencial para el torque tendremos,

\[ dT = dF~r= \frac{2 \pi \mu \omega}{y \sin \alpha} r^3~dr \]

\[ T = \frac{2 \pi \mu \omega}{y \sin \alpha} \int_0^R r^3~dr \]

Finalmente, luego de haber integrado dT entre 0 y T y el radio entre 0 y R resulta,

 

\[ \boxed{T = \frac{\pi \mu \omega r^4}{2 y \sin \alpha}} \]

Escribir comentario (0 Comentarios)

Visto: 4756

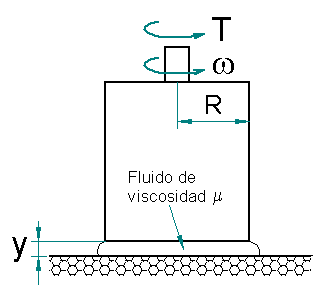
Se tiene un cilindro sobre una superficie como se ve en la Figura 1. Entre la superficie y el cilindro hay una capa de líquido con viscosidad

\[ \mu \]
y dicho cilindro gira a una velocidad angular constante
\[ \omega \]
determinada. La separación entre el cilindro y la superficie es "y", y el radio del cilindro es constante e igual a R.

 

Figura 1.

1. Aplicando la ecuación para el esfuerzo cortante, halle una expresión para hallar el torque T que se debe aplicar para mantener el cilindro girando. La expresión debe estar en función de

\[ \mu \]
, R,
\[ \omega \]
e y.

2. Teniendo en cuenta la expresión hallada para T, deduzca una para hallar la viscosidad

\[ \mu \]
.

Desarrollo

1. La expresión para el esfuerzo cortante es:

\[ \tau = \mu \frac{du}{dy} \]

Luego, tenemos que el esfuerzo es igual a un diferencial de fuerza sobre un diferencial de área,

\[ \frac{dF}{dA} = \mu \frac{du}{dy} \]

De donde,

\[ dF = \mu \frac{du}{dy} dA \]

Luego, al ser una distancia de separación pequeña podemos hacer,

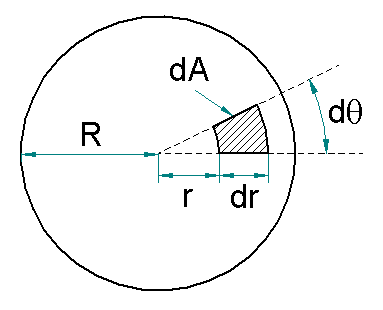
\[ \frac{du}{dy} = \frac{\Delta u}{\Delta y} = \frac{\omega r - 0}{y - 0} = \frac{\omega r}{y} \]

Al tener en cuenta el análisis diferencial expuesto en la Figura 2 deducimos que,

\[ dA = r~dr~d\theta \]

Figura 2. Análisis diferencial de la superficie del fondo del cilindro.

 Reemplazando los valores de dA y du/dy en dF resulta,

\[ dF = \frac{\mu \omega}{y} r^2 dr d\theta \]

Para hallar el torque necesitamos la ecuación diferencial para el torque, la cual es,

\[ dT = dF.r = \frac{\mu \omega}{y} r^3 dr d\theta \]

Integrando para hallar el valor de T,

\[ T = \int_0^T dT = \frac{\mu \omega}{y} \int_0^{2\pi} \int_0^R r^3 dr~d\theta \]

Finalmente,

\[ \boxed{T = \frac{\pi \mu \omega R^4}{2y}} \]

2. Como ya se tenía la expresión para el torque solo despejamos la viscosidad para dejarla en función del torque, la velocidad angular, la separación y el radio del cilindro, así:

\[ \boxed{\mu = \frac{2yT}{\pi \omega R^4}} \]

Escribir comentario (0 Comentarios)

Visto: 29290

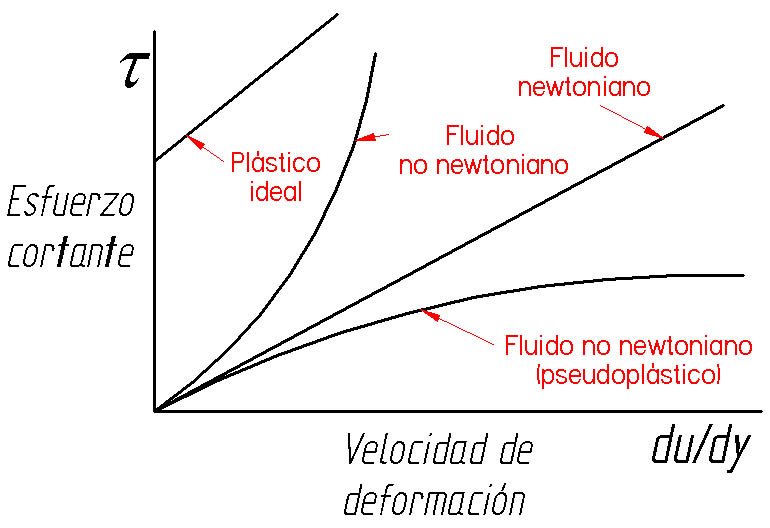
1. Fluidos Newtonianos

Los fluidos newtonianos son aquellos cuya viscosidad es constante o, dicho de otra forma, son aquellos cuyo esfuerzo cortante es directamente proporcional al gradiente de velocidad. Muchos fluidos comunes como el agua, el aire y el aceite son newtonianos.

2. Fluidos no Newtonianos

Tienen el esfuerzo cortante como función de relaciones de velocidad de deformación y tienen una composición molecular compleja.

3. Dilatantes

Son aquellos que se vuelven más resistentes al movimiento conforme se incrementa la velocidad de deformación.

4. Pseudoplásticos

Son aquellos que se vuelven menos resistentes al movimiento conforme se incrementa la velocidad de deformación.

Escribir comentario (0 Comentarios)

Visto: 2847

La viscosidad puede ser considerada como la pegajosidad interna de un fluido, como la medida de la resistencia que presenta un fluido a deformarse o como una medida de cuán bueno es un fluido para disipar energía como producto de un esfuerzo cortante.

Nos interesa conocer la relación que existe entre la velocidad de deformación de un fluido y su viscosidad.

Ley de Newton de la Viscosidad

A continuación se planteará una ecuación que relaciona el esfuerzo cortante aplicado con la viscosidad y su velocidad de deformación. Dicha ecuación es:

 

\[ \tau = \mu \frac{du}{dy} \]

O en su forma general,

\[ \tau = \mu \left( \frac{du}{dy} \right)^n + K \]

Donde el término de la izquierda es la letra tau y simboliza el esfuerzo cortante, la letra

\[ \mu \]
que es la viscosidad y el término du/dy que es la velocidad de deformación, donde u sería la velocidad y "y" la distancia de separación.

El significado del término es que al derivar la velocidad con respecto a la separación tendremos la pendiente de la gráfica que nos muestra a la velocidad en función de la separación. Para fluidos newtonianos esta gráfica es una línea recta.

Las unidades para el esfuerzo cortante son N/m2 o Pascales Pa.

Las unidades para la viscosidad son N.s/m2 o Pa.s.

Escribir comentario (0 Comentarios)