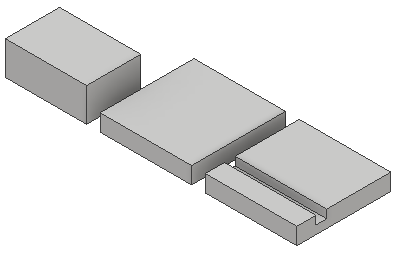
Para fabricar un componente para la industria se dispone de placas de acero inoxidable 20Cb-30 de 80 cm de ancho por 4 cm de espesor, previamente laminadas al 20% de trabajo en frío. Sobre estas placas, mediante forja, se imprime una cavidad de 20 mm x 20 mm x 80 cm de ancho.
1. Hallar el espesor (en mm) de la placa de acero inoxidable antes de ser laminada al 20%TF.
2. El trabajo en frío total efectuado para imprimir la cavidad rectangular y las propiedades mecánicas (en el sistema de unidades SI) que tendrá el material deformado bajo la cavidad (resistencia a tracción, resistencia a fluencia y % de elongación).
3. Si el material no fue recocido antes, ¿cuánta fuerza debió aplicar a la prensa de forja para imprimir la cavidad rectangular?
Desarrollo.
1. Naturalmente, tendremos en cuenta que hubo un trabajo en frío previo del 20%TF al momento de recibir la lámina. Gracias a esto podemos usar este dato y el espesor con el que nos suministran la lámina como un espesor final para hallar el espesor inicial, así:
$$20\%TF=\frac{e_0-40~mm}{e_0} \times 100\%$$
Despejando el espesor inicial obtenemos:
$$e_0=50~mm$$
2. En este punto solicitan el trabajo en frío total realizado luego de imprimir la cavidad rectangular. Se tiene en cuenta el estado inicial cuando se tenía 0%TF como estado inicial, así:
$$\%TF=\frac{e_0-e_{forja}}{e_0} \times 100\%$$
Tener en cuenta que \(e_{forja}\) es el espesor de la placa luego de la forja, es decir, aquel que se redujo debido a la compresión. Es el espesor de la placa bajo la cavidad rectangular.
$$\%TF=\frac{50~mm-20~mm}{50~mm} \times 100\%$$
$$\%TF=60\%$$
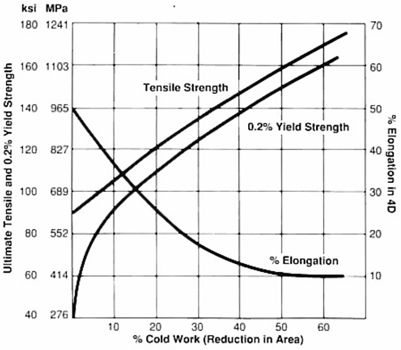
Las propiedades mecánicas a 60%TF son:
$$\sigma_U=\frac{1241~MPa + 1103~MPa}{2}=1172~MPa$$
$$\sigma_Y=1103~MPa$$
$$% elong=10\%$$
3. El material no fue recocido, luego, debemos tener en cuenta que la resistencia a fluencia que se debe superar para deformar plásticamente el material es la resistencia a fluencia cuando ya tiene 20%TF. Esta resistencia a fluencia es igual a:
$$\sigma_Y(20\%TF)=\frac{827~MPa+689~MPa}{2}=758~MPa=758\times10^6\frac{N}{m^2}$$
La fuerza que debió aplicarse para producir la plastificación del material para obtener la cavidad rectangular es:
$$P_{forja}=\sigma_{Y,20\%TF} \times A_{forja} =758 \times 10^6 \frac{N}{m^2} \times (20~mm \times 80~cm \times \frac{1~m}{1000~mm} \times \frac{1~m}{100~cm})$$
Luego,
$$P_{forja}=12128000~N = 12.13~MN$$




Comentarios potenciados por CComment