Descargue o visualice el ejercicio resuelto: Circunferencia_Ej_2.pdf

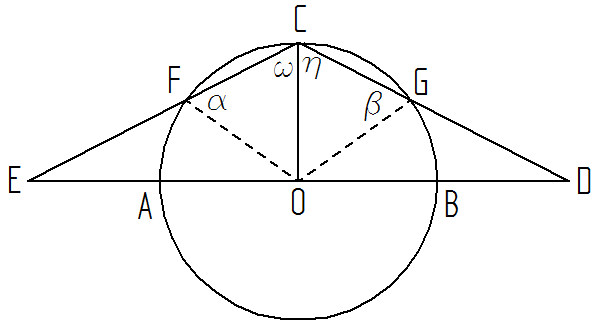
En una circunferencia se C(O,r) se traza un diámetro \(\overline{AB}\) y un radio \(\overline{OC}\) perpendicular a \(\overline{AB}\). Se prolonga \(\overline{AB}\) a cada lado y en el exterior de C(O,r) en longitudes iguales \(AE=BD\). Se trazan \(\overline{CE}\) y \(\overline{CD}\), que corta a C(O,r) en F y G. Probar que \(m(O \hat{F} C)= m(O \hat{G} C)\).

Hipótesis:
C(O,r).
\(\overline{AB}\): cuerda diametral.
\(\overline{OC}\) radio.
\(\overline{OC} \perp \overline{AB}\).
\(O-A-E\) y \(C-G-D\) con \(AE=BD\) (exteriores).
\(C-F-E\), \(C-G-D\).
\(F \wedge G \in C(O,r)\).

Tesis:
\(m(O \hat{F} C)=\alpha=\beta=m(O \hat{G} C)\).

Proposición - Razón

1. Trazo \(\overline{OF}\) y \(\overline{OG}\) Por construcción.

2. \(\overline{OA} \cong \overline{OB}\) (OA=OB) Por \(\overline{AB}\) cuerda diametral, por Hipótesis y definición de congruencia de segmentos.

3. \(\overline{AE} \cong \overline{BD}\) (AE=BD) Por Hipótesis y definición de congruencia de segmentos.

4. \(\overline{OC} \cong \overline{OC}\) Por propiedad reflexiva.

5. \(OE=OA+AE\) Por suma de segmentos.

\(OD=OB+BD\)

6. \(OE=OB+BD\) Por sustitución de 2 y 3 en 5.

7. \(OE=OD\) Por transitividad entre 5b y 6.

8. \(\overline{OC} \cong \overline{OC}\) Por propiedad reflexiva.

9. \(m(E \hat{O} C) = m(D \hat{O} C) = 90^o\) Por hipótesis. \(\overline{OC} \perp \overline{AB}\).

10. \(\triangle EOC \cong \triangle DOC\) Por criterio LAL. De 7, 8 y 9.

11. \(\overline{OF} \cong \overline{OC} \cong \overline{OG}\) Por ser segmentos radiales.

12. \(\triangle FOC\) y \(\triangle COG\) isósceles. Por 11 y definición de triángulo isósceles.

13. \(\alpha=\omega\) y \(\beta=\eta\) Por propiedad de triángulo isósceles. De 12.

14. \(\omega=\eta\) Por ser ángulos correspondientes en triángulos congruentes. De 10.

15. \(\alpha=\beta\) Por transitividad en 13 y 14. l.q.q.d.