Demostrar que la longitud de la mediana de un triángulo está comprendida entre la semisuma y la semidiferencia de los lados que parten del mismo vértice.
Hipótesis
\(\triangle ABC\) cualquiera.
\(\overline{AM}\) mediana.
Tesis
$$ \frac{AC-AB}{2}<AM<\frac{AB+AC}{2} $$
| Proposición | Razón | |
| 1. | Hipótesis. | Por hipótesis. |
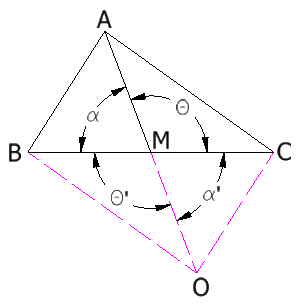
| 2. | Trazo prolongación \(\overline{MO}\) de \(\overline{AM}\), con \(\overline{MO}\cong \overline{AM}\) (luego, \(MO=AM\)). | Construcción auxiliar y definición de congruencia de segmentos. |
| 3. | Trazo \(\overline{BO}\) y \(\overline{OC}\) | Construcción auxiliar. |
| 4. | \(\alpha = \alpha'\) | Ángulos opuestos por el vértice M (A-M-O y B-M-C). |
| \(\theta = \theta'\) | ||
| 5. | MB=MC | Por \(\overline{AM}\) mediana (hipótesis). Por definición de mediana de un triángulo. |
| 6. | \(\triangle MAC \cong \triangle MOB\) | Criterio LAL. De 2, 4 y 5. |
| \(\triangle MAB \cong \triangle MOC\) | ||
| 7. | AC=BO a) | Lados homólogos entre triángulos congruentes. De 6. |
| AB=CO | ||
| 8. | AO=AM+MO | Suma de segmentos adyacentes. |
| 9. | AO=2AM | Sustitución de 2 en 8 y propiedad de los reales en lado derecho. |
| 10. | AO<AB+BO | Teorema de desigualdad triangular. |
| 11. | 2AM<AB+AC | Sustitución de 9 en 10 (lado derecho) y de 7 en 10 (BO=AC). |
| 12. | AM<(AB+AC)/2 | Propiedad de las desigualdades. De 11. Parte de lo que queremos demostrar. |
| 13. | AO>|AB-BO| | Teorema de desigualdad triangular. |
| 14. | 2AM>|AB-AC| | Sustitución de 9 en lado izquierdo de 13 y 7a en lado derecho de 13 (BO=AC). |
| 15. | AM>|AB-AC|/2 | Propiedad de las desigualdades. De 14. |
| 16. | |AB-AC|/2<AM<(AB+AC)/2 | Propiedad de las desigualdades (transitiva). De 12 y 15. |




Comentarios potenciados por CComment