17. (Dificultad: 6/10) Considere los puntos $A-M-B-N$ que cumplen con la siguiente condición:

$\frac{AM}{BM}=\frac{AN}{BN}$

Si $O$ es el punto medio de $\overline{AB}$ , demostrar que:

$(OA)^2=OM.ON$

Solución

$1.~A-M-B-N$

$2.~\frac{AM}{BM}=\frac{AN}{BN}$

$3*.~\text{O punto medio de}~\overline{AB}$

$(OA)^2=OM.ON$

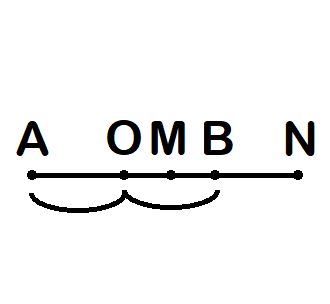
	Proposición	Razón
3.	$AM=OA+OM$	Por suma de segmentos adyacentes.
4.	$BM=OB-OM$	Por suma de segmentos adyacentes.
5.	$AN=OA+ON$	Por suma de segmentos adyacentes.
6.	$BN=ON-OB$	Por suma de segmentos adyacentes.
7.	$\frac{OA+OM}{OB-OM}$ $=\frac{OA+ON}{ON-OB}$	Sustitución de 3, 4, 5 y 6 en 2 (hipótesis).
8.	$OB=OA$	De 3* (hipótesis). Por la definición de punto medio de un segmento.
9.	$\frac{OA+OM}{OA-OM}$ $=\frac{OA+ON}{ON-OA}$	Sustitución de 8 en 7.
10.	$(OA+OM)(ON-OA)$ $=(OA+ON)(OA-OM)$	De 9. Por propiedad de los reales.
11.	$OA.ON-OA^2+OM.ON-OM.OA$ $=OA^2-OA.OM+ON.OA-ON.OM$	De 10.
12.	$2OM.ON=2OA^2$	De 11.
13.	$OA^2=OM.ON$	De 12. Por propiedad de los reales. TESIS.

Comentarios potenciados por CComment

Ejercicio resuelto 17 | Segmentos | Punto medio y proporción