Descargue el ejercicio resuelto en formato .pdf: Circunferencia_Ej_18.pdf

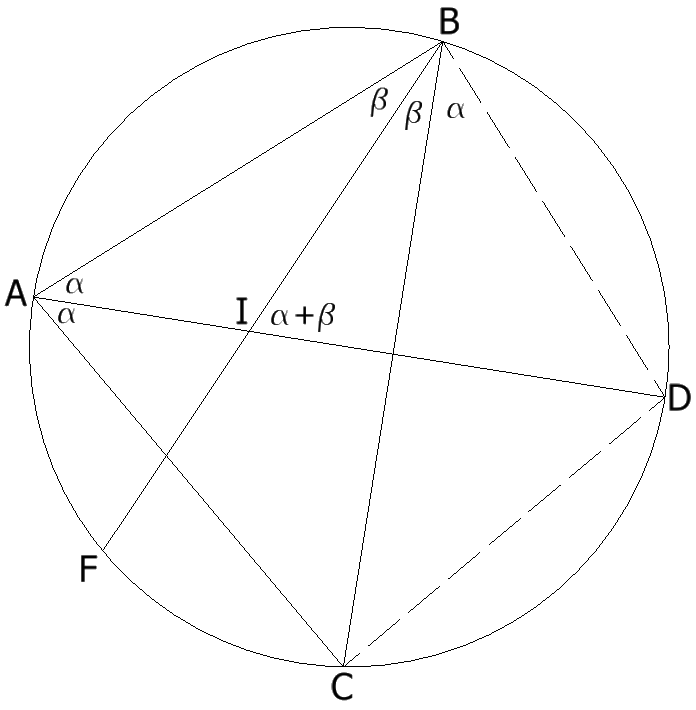
Se tiene un \(\triangle ABC\) inscrito en una C(O,r). Se trazan las bisectrices de los ángulos A y B, que se intersectan en I y que encuentran a la circunferencia en D y F. Demostrar que \(\overline{DI}=\overline{DB}\).

Hipótesis:

\(\triangle ABC\) inscrito en C(O,r).

\(\overline{BF}\) y \(\overline{AD}\) bisectrices de \(\hat{A}\) y \(\hat{B}\).

\(\overline{AD} \cap \overline{BF} = I\)

\(\overline{BF} \cap C(O,r) = F\)

\(\overline{AD} \cap C(O,r) = D\)

Tesis:

\(DI=DB\)

 Proposición - Razón

1. Trazo \(\overline{DB}\) y \(\overline{DC}\). Por construcción.

2. \(m(B \hat{A} D) = m(D \hat{A} C) = \alpha\) Por Hipótesis (AD es bisectriz ang. A).

3. \(m(A \hat{B} F) = m(F \hat{B} C) = \beta\) Por Hipótesis (BF es bisectriz de ang. B).

4. \(m(D \hat{A} C)=\alpha=\frac{1}{2} m(\overset{\frown}{DC})\) Por Teorema del ángulo inscrito (un ángulo inscrito mide la mitad del arco comprendido entre sus lados, ver documento gu'ia).

5. \(m(C \hat{B} D)=\frac{1}{2} m(\overset{\frown}{DC})\) Por misma razón de 4.

6. \(m(D \hat{A} C)=m(C \hat{B} D)=\alpha\) Por transitividad entre 4 y 5.

7. \(m(B \hat{I} D)=\alpha + \beta\) Por Teorema del ángulo exterior de un triángulo (es igual a la suma de los ángulos interiores no adyacentes). El triángulo es el \(\triangle\) ABI.

8. \(m(F \hat{B} D)=m(C \hat{B} D) + m(F \hat{B} C)\) Por suma de ángulos.

9. \(m(F \hat{B} D)=\alpha + \beta\) Por sustitución de 6 y 3 en 8.

10. \(m(F \hat{B} D)=m(B \hat{I} D)\) Por transitividad entre 7 y 9.

11. \(\triangle BID\) es isósceles con base \(\overline{BI}\) Por propiedad del triángulo isósceles (Teorema: un triángulo es isósceles si y solo si tiene dos ángulos congruentes). De 10.

12. \(DI=DB\) De 11. (L. q. q. d).