El siguiente archivo está constituido por tres ejercicios para poner en práctica las construcciones que se verán a continuación: Practica_construcciones_geometricas.pdf
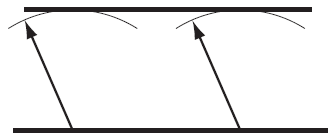
Construir una línea paralela a otra
Para ello trazamos dos arcos separados cuyo radio es la separación entre las dos líneas.
Bisectar una línea
Para ello realizo arcos con centro en los extremos de la línea que deseo dividir en dos partes iguales. Estos arcos deben tener un radio mayor a la mitad de la línea. El punto medio estará definido al unir los dos puntos que resultan del cruce de los arcos a cada lado.
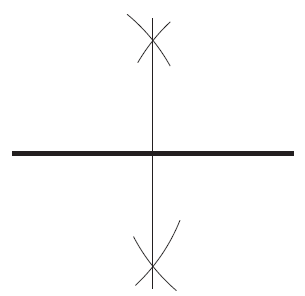
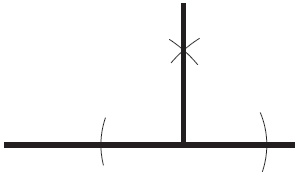
Construir una línea perpendicular a otra
Debo tener identificado el punto sobre la línea a partir del cual trazaré la perpendicular. Luego, abro el compás cualquier medida y trazo dos pequeños arcos a lado y lado sobre la línea. Luego, estos puntos de cruce entre los arcos y la línea se toman como centro y se trazan dos arcos, uno por cada punto de cruce. La perpendicular se obtiene al unir el punto de origen con el punto de cruce entre los dos arcos que se acaba de hallar (es la X en el dibujo).
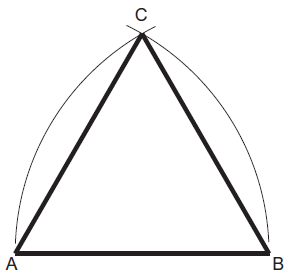
Construir un triángulo equilátero dado un lado de longitud conocida
Supongamos que se conoce el lado AB. Con centro en A trazo un arco de radio AB. Luego, con centro en B, trazo otro arco de radio AB. El cruce ambos arcos produce el punto C. Por último, uno A, B y C para formar el triágulo equilátero.
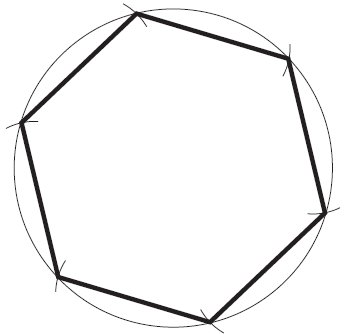
Construir un hexágono regular dado un lado de longitud conocida
Primero dibujo un círculo de radio igual al lado de longitud conocida. Luego, desde cualquier punto de la circunferencia (elegir el que sea más conveniente) trazar seis arcos sobre la circunferencia, tomando los puntos de corte entre circunferencia y arco como centro del arco siguiente hasta completar los seis puntos. Por último, sólo se deben unir estos puntos de cruce.
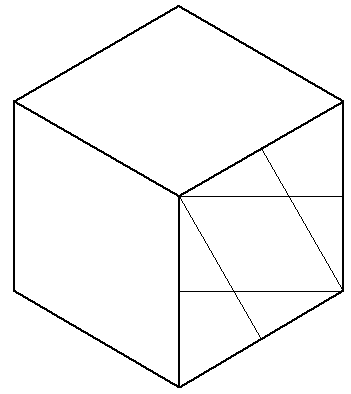
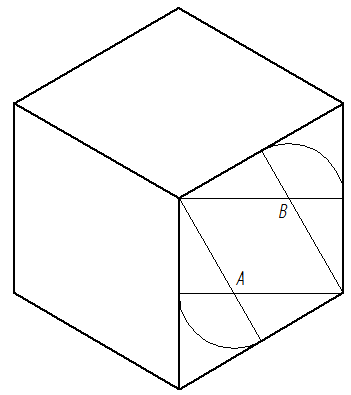
Construir una elipse sobre las caras de un cubo en vista isométrica
En la vista isométrica del cubo tendremos que la longitud de todos los lados es la misma (esto se asume por simplicidad). Para iniciar seleccionamos cualquiera de las caras. Luego, identificamos los dos puntos que están sobre la línea que pasa a través del eje menor de la elipse. Otra manera de verlo es seleccionar los dos puntos no consecutivos más cercanos entre sí de esa cara. A continuación, desde cada punto se trazan dos líneas hasta los puntos medios de los lados opuestos.
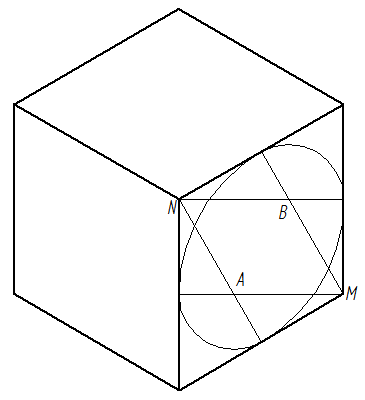
Luego, con centro en los puntos de cruce A y B se abre el compás y se trazan los arcos (de punto a punto) que se observan en la siguiente figura.
Finalmente, tomando como centro los puntos N y M, se abre el compás y se trazan los dos últimos arcos.
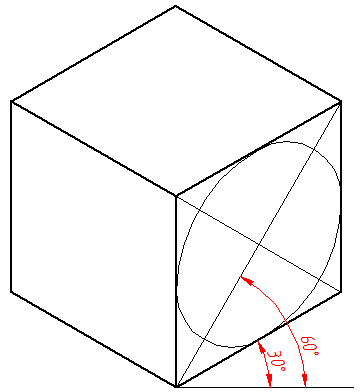
El procedimiento anterior es útil para dibujar una elipse sobre cualquiera de las tres caras del cubo isométrico. Nótese que el ángulo entre el eje mayor de la elipse y la horizontal es de 60°. Es decir, la inclinación de una elipse dibujada sobre las caras de un cubo isométrico es de 0°, 60° ó 120°.
En el video que se observa a continuación se aprecia el uso de las técnicas:
Arco tangente a dos círculos
Primera alternativa
Dado el radio \(R\) del arco y los radios de las circunferencias \(C1\) y \(C2\), el problema a resolver consiste en hallar el punto \(C\):
1. Con centro en \(A\), trazar un arco de radio (arco color rojo):
$$ R1=C1+R $$
2. Con centro en \(B\), trazar un arco de radio (arco color verde):
$$ R2=C2+R $$
El punto de intersección entre los dos arcos es \(C\).
3. Con centro en \(C\), se traza el arco deseado de radio \(R\), el cual debe quedar dibujado tangente a ambas circunferencias.
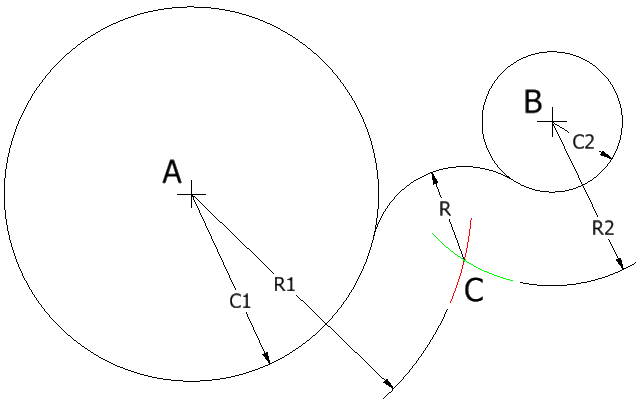
Figura 1. Primera alternativa para el dibujo de un arco tangente a dos circunferencias.
Segunda alternativa
Dado el radio \(R\) del arco y los radios de las circunferencias \(C1\) y \(C2\), el problema a resolver consiste en hallar el punto \(C\):
1. Con centro en \(A\), se traza un arco de radio (arco color rojo):
$$ R1=R-C1 $$
2. Con centro en \(B\), se traza un arco de radio (arco color verde):
$$ R2=R-C2 $$
El punto de intersección entre los dos arcos es \(C\).
3. Con centro en \(C\), se traza el arco deseado de radio \(R\), el cual debe quedar dibujado tangente a ambas circunferencias.
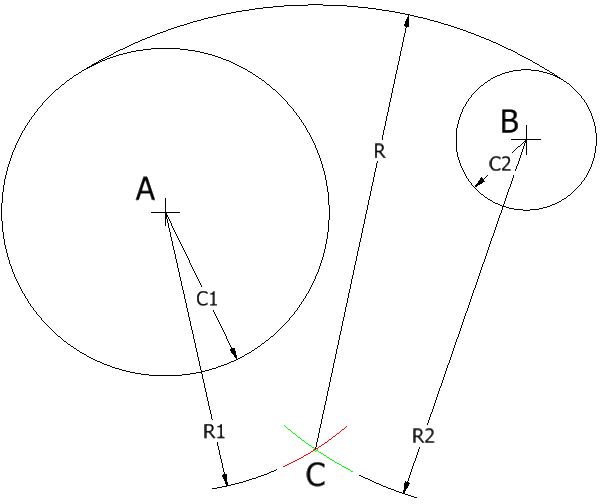
Figura 2. Segunda alternativa para el dibujo de un arco tangente a dos circunferencias.
En el video que se observa a continuación se aprecia el uso de la técnica:




Comentarios potenciados por CComment